Hi all,
A few years ago, the city tore down the playground by my house and built another one that wasn't as good. Today's post is about showing mathematically why I believe that to be the case. My theory is that better playgrounds aren't necessarily larger, or have more features, but rather, their graphs contain more directed cycles.
But also, let's be honest. I don't know much about cyclic graph analysis. I just wanted to use some fancy words in the headline and draw diagrams of playgrounds.
In plain English, it's the number of paths that you can take through a play structure that make it more fun and interesting for play.
The playground, then and now.
Let's take a look at the new playground, curtesy of Google Maps Street View. It's a basic, dual tower structure, connected by a bridge.

For a picture of the old playground, Street View also has the ability to go back in time, but the image from the best point of view was blocked by a truck parked in the way. Fortunately, the internet never forgets and I found a ten year old blog from someone trying to visit every single park in Somerville and that's where this photo is from.

The Diagrams
These are the two playgrounds, drawn as top down views. Clearly, the older one has more platforms, so intuitively, it should be better, but that playground in particular was exceptionally fun, even when compared to larger structures.
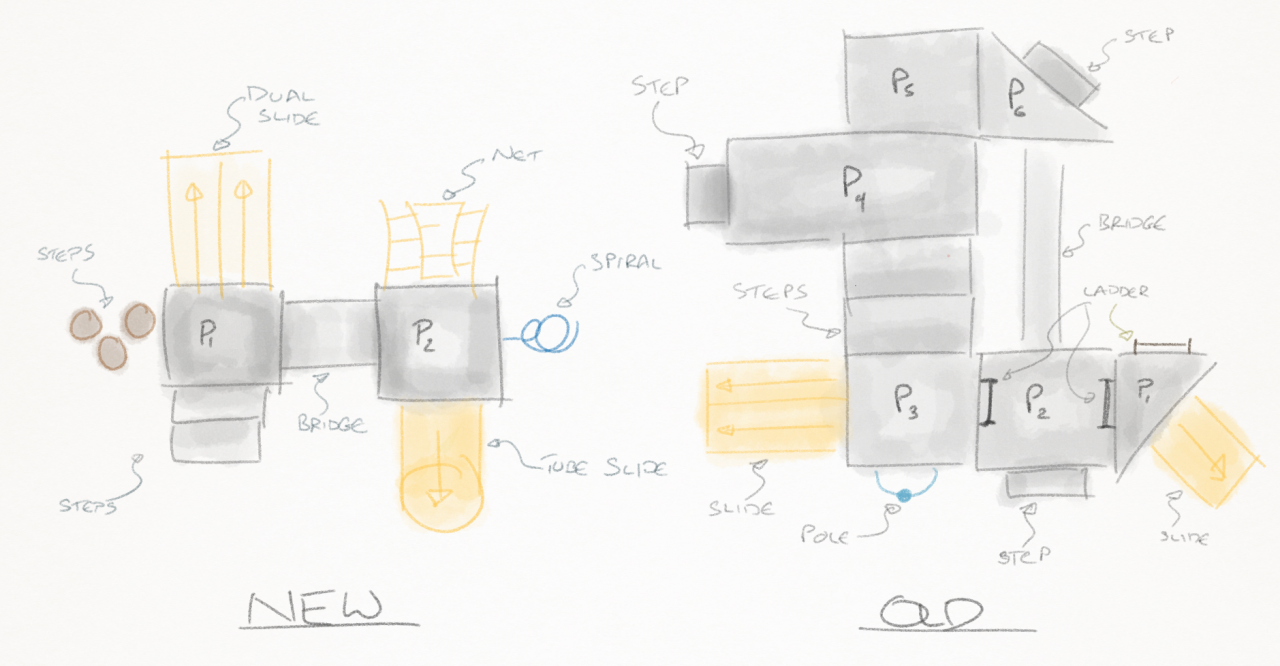
The Graph
To explain why, I've redrawn the playground as a directed graph. Each platform becomes a "node" and each pathway onto or off the platform becomes an "edge". The ground in this case is one large node. The edges are "directed" because it's possible to go down slides and fire poles, but not up them. (My children, like all children, would argue this point, and insist that going up the slides is indeed possible, and a fun challenge.)

The old playground clearly had multiple loops, or "cycles", both through and around the structure. That's what made it so much fun. It's the bridge path from P2 to P6 that really makes it. You're not confined to a dull back and forth, but you're faced at each entry point with the possibility of choice, to go left OR go right.

Recommendation
Of course, I recognize that there are resource constraints on materials and playground budgets, but if there was an opportunity, I would absolutely advocate to add a leg, or fork, or some other variant to increase the number of paths through the play structure, rather than just making it bigger.
And that's how the AwkEng applies cyclic graph analysis to playground design.
Best regards!
Sam
aka THE Awkward Engineer
